小1コドモが「引き算嫌だ~」と言ってます。^^
特に、繰り下がりのある引き算が嫌なようで。^^
「こヤツ(我がコドモ)はもしかして
量的感覚(数を数字ではなく、
量としてイメージできる能力の意味で使ってます)を
あまり持ってないタイプなのかしらん?」と思う感じで
宿題プリントをやる時には必ず「嫌だ~」と騒いでおります。^^
(引き算習い始めの自分のことは全く覚えていないし、
平均でどれくらいなものなのかもわからないので、
何とも言えませんが・・・)
20個分のブロックを目の前に出して計算するのもイマイチ
気分が乗ってこないようです。

今までのところ、
『19までの数 ー 9までの数』の引き算のみ習っています。
コドモのようすを見ていると、
繰り下がりのある計算の中でも
答えが9になる問題については、ほぼ反射的? な
感じでできるみたいです。
14ー5とあったら、
1の位からとりあえず4を引くのと同時に?
10からも1を引いて9と答えを出せているよう。
「1引けばいいから」と本人が言っていますので。
何となく5は4より1多い、ということを瞬時に判断しているのかな?
15ー7のように、答えが8になるような問題だと、
まだ瞬時にはイメージ? できないみたいです。
そもそも、1桁どうしの引き算も
まだ頭の中で1ずつ引いているみたいなので、
そこからですかね、多分。
9ー1は、9から1減らすだけだから、答えがすぐ8と出せるけど、
9ー2になると、9から1を減らして、もう一度1を減らして、
と1つずつ頭の中で数えているようなので、
単純計算で、9-1の2倍の時間がかかっている感じです。
それが9ー3だと3倍、・・・となっていくようです。
9の塊から2の塊を一気に減らして7の塊、
9の塊から3の塊を一気に減らして6の塊、とはなっていないようです。
ま、これからかな? 多分?^^
ある日、学校の授業で使ったと思われるプリントに、
お! と思うものを見つけました。
こんな内容です。
問題文:
答えが10になるカードに赤色を塗りましょう。
答えが2から9までのカードを青色で囲みましょう。
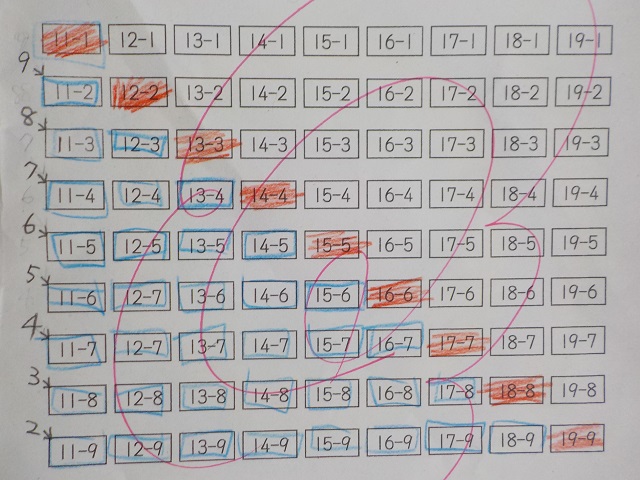
(よく見ると、12ー6 と書きたいはずのところが 12ー7 となってますね^^)
赤に塗った部分は10になり、
その1段下は斜めに全カード答えは9、2段下は8、3段下は7、・・・と
以下続いていきます。
「この中から同じ問題探せば答えわかるんじゃない?」
と言ってみたら、ちょっとモチベーションが上がったみたいで、
時折、探しつつ「嫌だ~」とは言わずにやっていました。
探すのもメンドクサイ? ともチラッと思いましたが。^^
そこは大丈夫みたいでした。
実際に問題に取り組む時には、
このプリントが手元にあるわけではないので
邪道なような気もします。
でも、数の法則性? みたいなものをイメージする一助になるような
気もするのですが、どうですかね?
なんてことを思っていたら、こういった内容の一覧が
学習ポスターとして販売もされているのですね。
しかも九九のように暗唱して覚えさせるといった意図も
あったりするようで。
オットは元々
「もう九九みたいな感じで引き算も
覚えちゃったほうがはやいんじゃない?」
と言っています。
ワタシは基本的には
「まずは数を量として思い浮かべる練習からしておいたほうが
いいんじゃないかな~」
と思っていて、
かつ、引き算を覚えるという発想がこれまで全くなかったし、
今もないので、よくわからない、ということがありました。
じゅういちひくにはきゅう
って丸暗記できるもの? それ全部覚えるの?
無理でしょ! ってな感じで。^^
まぁ、九九と一緒で子どものうちにやればできる気もします。
もしも子どもが喜んでチャレンジするなら、の話かなぁ。
そしてスタートは暗記だったとしても、
数の量的感覚もある程度はあったほうが何かと楽そうだと思いますし。^^
オットが「俺は覚えちゃってる」と言うので、
あんまり納得できず、詳しく追及してみたら
「勉強している途中で、覚えたほうがはやいと気づいて
それから自分で覚えていくようにした。
例えば、15-8とかは覚えにくいんんだけど、
大体7くらいかな、と見当つけてとりあえず7を書いて、
後で、7+8を計算して、確かに15になるなと確かめていく感じで、
段々身につけていった。
『じゅうごひくはちはなな』と覚えたわけではないよ。」
「いちいち検算するの?
でも、その足し算も覚えちゃってるわけ?」
しばし沈黙。
「究極的にはブロックかなぁ。
ブロック足してるのかなぁ」
ほらぁ、やっぱりイメージ先行でしょ~、
と思ったのでした。が、どうなんですかね?
しかしながら・・・。
暗記ということで言えば
インドでは九九を20の段まで暗記してしまう。
そして、インドは理数系に強い人間が多い、と。
どの程度相関があるものなのか全くわかりませんが、
そういう話は聞いたことあります。
まぁ、このプリントに関しては
丸暗記するかどうかはちょっと置いておいても、
何となく全体図をイメージできるっていうのは悪くないかな、
と思いました。
法則性を見つける、知るって大事な要素だと思うので。
これを使うことで、コドモのモチベーションが少し上がり、
そのうち何となく自然にイメージできるようになってくれば
万々歳かな、と思っているのですが、
しばらく、引き算をする時の参考資料として
傍には置いておこうと思います。
さて、どうなりますことやら・・・^^。
と~っても興味深いです。^^
算数的な話。
2×3のブロックとメロンパン(かけ算と引き算) - 好きに暮らす -now or never-
【コドモの量的感覚】かぞえないでかくよ - 好きに暮らす -now or never-